M. Puech, M. Streho
Le calcul d’implant après chirurgie réfractive reste un art difficile de par la multiplicité des techniques de chirurgie réfractive sur des yeux d’anatomies différentes et des réfractions traitées. La modélisation est donc hasardeuse et les différentes techniques de calcul proposées tendent à améliorer les résultats obtenus en moyenne, sur un échantillon donné, mais la dispersion des résultats reste souvent importante.
L’objectif de l’emmétropie postopératoire après chirurgie de la cataracte sur des yeux opérés de chirurgie réfractive reste un but atteint de façon majoritaire mais sans véritable reproductibilité en fonction de chaque cas. Le rajout d’une exigence de multifocalité après chirurgie du cristallin, sur ces patients sélectionnés pour leur exigence de qualité de vision, représente un défi important pour les années à venir. Ce but est cependant incontournable pour s’élever au niveau des technologies actuellement disponibles en matière de correction de la presbytie.
Quelle que soit la technique de calcul employée, le principe de la prédiction de la réfraction postopératoire repose sur l’utilisation de formules de calcul fondées sur des valeurs mesurées ou estimées à partir de constatations faites sur les yeux de ces patients candidats à une chirurgie du cristallin.
Le calcul d’implant est donc indissociable du couple formé par la formule de calcul et les mesures nécessaires à la bonne mise en œuvre de cette formule.
L’évolution des formules se fait en fonction des technologies disponibles, en tenant compte des spécificités à la fois des appareils de mesures et des éléments technologiques des implants utilisés. Cette chaîne complexe ne donne son optimum que lorsque chaque maillon est analysé avec précision et que les différents éléments restent cohérents entre eux. Cette cohérence de la chaîne de calcul fait l’objet d’adaptations et de correctifs souvent dévolus à la constante A. Cette constante décrite avec les premières formules de calcul, dites de régression, permet souvent de réajuster des éléments variables comme les différences de mesure de longueur axiale, soit en mode ultrasonore soit en mode optique, les différences de mesure de la puissance cornéenne, les différences d’appréciation de la position de l’implant. La constante A se comporte souvent comme une « boîte noire » censée compenser tous les éléments aléatoires du calcul, avec nécessité de l’adapter à la technique chirurgicale, à l’implant utilisé, à la formule choisie et au chirurgien. Ces multiples paramètres font évoluer la notion de constante A vers la notion de variable A assez difficile à appréhender.
En fonction de chaque situation, il est nécessaire d’analyser les paramètres cruciaux du calcul d’implant et les risques d’erreur liés à cette situation donnée.
Le calcul d’implant standard et le calcul d’implant visant à compenser la presbytie obéissent aux mêmes règles, avec une exigence plus grande dans la recherche de l’emmétropie en cas de chirurgie de la presbytie.
Depuis la première formule SRK, les formules de calcul ont évolué régulièrement, avec une meilleure appréciation de la position de l’implant en postopératoire et en prenant plus de mesures sur les yeux du patient candidat à l’opération de la cataracte.
Le calcul de la puissance des implants intraoculaires repose sur l’utilisation de formules mathématiques de plus en plus précises. De nombreux facteurs interviennent dans le résultat réfractif post-opératoire. La plupart de ces facteurs peuvent être mesurés en préopératoire, comme la kératométrie et la longueur axiale, qui sont les deux mesures pratiquées couramment. Cependant, l’évolution des formules de calcul se fait vers la personnalisation des mesures pour chaque patient, avec l’intégration de valeurs préopératoires additionnelles, comme la profondeur de la chambre antérieure phake (ou préopératoire), l’épaisseur du cristallin, le diamètre cornéen horizontal, la réfraction préopératoire et l’âge du patient.
L’amélioration de la prédictibilité de la réfraction postopératoire se fait sur deux axes : l’amélioration des formules de calcul et l’amélioration de la précision des mesures préopératoires.
La base de la précision des différentes formules de calcul repose sur l’appréciation de la position effective de l’implant dans un globe oculaire de dimensions connues. Cette position de l’implant intraoculaire dépend de trois éléments : la géométrie de l’implant, l’anatomie de l’œil opéré et la précision du geste chirurgical lors de l’implantation.
La géométrie de l’implant représente un élément important dans la prédiction de la réfraction et, surtout, dans la reproductibilité des résultats.
L’anatomie de l’œil à implanter va influer directement sur la position de l’implant ; en effet, la position du cristallin et son épaisseur peuvent être différentes pour des yeux de même longueur axiale, ce qui entraîne une variation de la position de l’implant intraoculaire et donc une variation de la réfraction finale.
La généralisation de la phacoémulsification avec implantation dans le sac capsulaire réduit la variabilité de positionnement des implants, pour un même opérateur mais aussi entre différents opérateurs. Ce progrès technique incontestable s’accompagne d’une récupération visuelle rapide, dont le corollaire est une constatation tout aussi rapide des erreurs de calcul prédictif. S’agissant de patients opérés à visée réfractive, l’objectif de perfection dans le calcul d’implant doit s’appliquer à toutes les étapes de cette chirurgie.
Les deux paramètres principaux du calcul d’implant, à savoir la kératométrie et la longueur axiale, font donc l’objet d’études plus approfondies qui bénéficient des progrès de nouveaux appareillages comme la vidéokératoscopie et les kératomètres automatiques, les analyses par Scheimpflug camera, par ray-tracing ou OCT, d’une part, et la biométrie guidée par l’échographie en mode B et l’interférométrie d’autre part.
Le calcul d’implant se fait à partir de données mesurées sur l’œil à implanter et de données caractéristiques de l’implant qui sera utilisé. Schématiquement, les formules de calcul se divisent en deux grandes catégories : les formules théoriques et les formules de régression.
Les formules théoriques font appel aux lois de l’optique géométrique avec détermination du pouvoir optique d’un système optique complexe. Ces calculs nécessitent de connaître les indices de réfraction des milieux traversés ainsi que la position des plans optiques principaux.
Les formules de régression linéaire sont fondées sur une étude statistique de résultats réfractifs obtenus avec tel ou tel type d’implant.
Les calculs optiques décrits par Gauss en 1841 servent toujours de base aux formules de calcul d’implants intraoculaires [12]. C’est Fyodorov qui, en 1967, a décrit la première application moderne de l’optique gaussienne au calcul des implants intraoculaires [7]. Ces calculs reposent sur des formules théoriques que plusieurs auteurs ont progressivement adaptées. La famille des formules théoriques utilise six variables : la puissance optique cornéenne totale (K), la longueur axiale (AL), la puissance optique d’un implant théorique sans épaisseur (IOLP), la position effective de cet implant (ELP), la réfraction désirée (R) et la distance du vertex du verre correcteur (V).
La base de ces formules théorique s’écrit1 :

La relative complexité de mise en œuvre des formules théoriques a poussé Sanders, Retzlaff et Kraff à proposer, en 1980, une formule plus simple d’utilisation fondée sur l’analyse statistique de grandes séries de patients opérés [29].
Il s’agit d’une formule de régression linéaire, dénommée formule SRK, qui s’écrit :
IOLP = A – 0,9 × K – 2,5 × L
avec comme variables la longueur axiale (L) et la kératométrie (K), la constante A résumant les caractéristiques de l’implant, notamment la position de l’implant par rapport à la cornée. Cette formule permet, avec seulement deux variables, de calculer rapidement la puissance d’un implant de constante A connue. Malheureusement, si les résultats réfractifs obtenus avec les formules de régression sont assez précis pour des valeurs moyennes de kératométrie et de longueur axiale, ils deviennent beaucoup moins précis pour les globes oculaires hors norme. Une première adaptation de la formule SRK a été proposée, par les mêmes auteurs, pour corriger les erreurs de calcul constatées pour les yeux myopes et hypermétropes : cela a donné naissance à la formule SRK II, qui modifie les résultats de la formule SRK en fonction de la longueur axiale [31].
La formule SRK II a fait référence pendant de très nombreuses années mais la constatation de résultats qui restent moins précis pour les yeux hors norme et la vulgarisation des équipements informatiques a permis un retour vers les formules théoriques et l’abandon progressif des formules de régression linéaire. Sanders, Retzlaff et Kraff sont eux-mêmes revenus aux formules théoriques en développant en 1990 la formule SRK/T qui, malgré une appellation trompeuse, est radicalement différente de la formule SRK II [30].
La tendance actuelle est donc d’améliorer la précision des formules théoriques, surtout par une meilleure appréciation de la véritable position de l’implant dans l’œil à opérer.
En 1981, Binkhorst a affiné la prédiction de la position de l’implant en corrélant la position effective de l’implant à la longueur axiale, ouvrant ainsi la voie à la deuxième génération de formules théoriques [2].
En 1988, Holladay a montré une amélioration des résultats par une corrélation de la position de l’implant avec, non seulement la longueur axiale, mais aussi la kératométrie, ce qui correspond à la troisième génération de formules théoriques [18].
En 1995, Olsen a publié une formule qui apprécie la position de l’implant pour un patient donné à partir de quatre variables : la longueur axiale, la kératométrie, la profondeur de chambre antérieure préopératoire et l’épaisseur du cristallin [28].
En 1996, Holladay a modifié sa formule dans le but d’améliorer les résultats pour les globes très courts : la formule de Holladay 2 intègre la profondeur de la chambre antérieure préopératoire, le diamètre cornéen de blanc à blanc et l’épaisseur du cristallin [8, 22].
Haigis a écrit une formule de calcul adaptée à l’appareil IOLMaster®, cette formule optimise le calcul d’implant en tenant compte des valeurs mesurées par cet appareil (kératométrie, profondeur de chambre antérieure, longueur axiale par interférométrie et distance de blanc à blanc) [13]. L’adaptation de la constante A à cette formule et à cet appareillage fait l’objet d’une mise à disposition des études sur le site internet ULIB2, de façon à adapter les constantes utilisées avec telle ou telle formule en fonction de tel ou tel implant.
Cette évolution des formules se fait vers une meilleure intégration des véritables mesures de l’œil à implanter, ce qui a comme corollaire la nécessaire amélioration de la précision des mesures préopératoires.
Le principe de ces formules est de ramener le système optique oculaire à une association de deux lentilles simples, l’une représentant la cornée et la seconde représentant l’implant intraoculaire. Le pouvoir optique de ce système doit entraîner la focalisation des images sur le plan des photorécepteurs de la fovéola.
La cornée présente deux dioptres principaux : un antérieur entre l’air et la face antérieure cornéenne, puis un second dioptre entre face postérieure de la cornée et humeur aqueuse. Dans les formules de calcul, la cornée est ramenée à un dioptre théorique unique séparant l’air de l’humeur aqueuse avec un plan principal secondaire situé à 0,05 mm de la surface cornéenne.
L’implant est lui aussi ramené schématiquement à une lentille simple de faible épaisseur, qui représente la résultante des deux dioptres véritables de l’implant : celui entre humeur aqueuse et face antérieure de l’implant et celui entre face postérieure de l’implant et humeur aqueuse.
Un débat récent semble prôner le retour vers l’utilisation de modèles optiques non plus fondés sur le modèle de la lentille optique fine pour schématiser les différents éléments du système optique de l’œil, mais sur un modèle de lentille épaisse reposant sur des mesures directes des rayons de courbure et des épaisseurs des différents éléments que sont la cornée et le cristallin. Ce changement sur le fondement même des formules accompagnera vraisemblablement le calcul d’implant plus complexe en cas de chirurgie réfractive et en cas de compensation de la presbytie, mais il nécessite des outils adaptés pour les mesures d’épaisseur et de rayons de courbure, par exemple, des faces antérieure et postérieure de la cornée et du cristallin.
Les résultats du calcul d’implant sont souvent présentés sur la base des valeurs de la différence entre la réfraction souhaitée en préopératoire et la véritable réfraction obtenue en postopératoire. Ils sont plus souvent exprimés en pourcentage d’erreur réfractive, compris entre ± 0,50 D, ± 1,00 D, ± 2,00 D ou ± 3,00 D, par rapport à l’objectif visé.
En 1992, Holladay présentait le standard de la technique de chirurgie de cataracte simple fondé sur la biométrie en mode A comme étant de 50 % des patients à ± 0,50 D de la réfraction souhaitée, 90 % à ± 1 D et 99 % à ± 2 D [21].
L’arrivée des systèmes optiques de mesure de longueur axiale couplés à une mesure de kératométrie et de la profondeur de la chambre antérieure, comme l’appareil IOLMaster® (Zeiss-Meditec), a permis d’améliorer sensiblement les résultats à 62,5 % des patients à ± 0,50 D de la réfraction souhaitée, 92,4 % à ± 1 D et 99,9 % à ± 2 D.
L’apport de la biométrie optique a donc assez nettement augmenté le pourcentage de patients à ± 0,50 D mais en laissant cependant encore près de 38 % des patients en moyenne avec une amétropie supérieure à 0,50 D. Cet élément fait comprendre l’aléa qui persiste dans l’objectif réfractif en cas de traitement de la presbytie par nos techniques actuelles.
La mesure des rayons de courbure de la cornée représente un des éléments essentiels du calcul d’implant. Cette mesure peut être réalisée par différents instruments, mais la kératométrie sur le principe de Javal représente la référence de nombreuses formules de calcul d’implant. Avec un kératomètre de Javal, les mesures sont prises en projetant, sur la zone cornéenne centrale, deux mires distantes d’environ 3 mm. Cette distance entre les deux mires varie en fonction de la courbure cornéenne : plus la cornée est courbe et plus la mesure s’éloigne du centre. La rotation à 90° des deux premières mires permet d’obtenir une mesure supplémentaire portant à quatre points de mesure les informations données par les kératomètres de type Javal.
Comme les kératomètres manuels, les kératomètres automatiques mesurent les quatre points de kératométrie sur les 3 mm centraux. La tendance actuelle est d’utiliser les valeurs obtenues par les systèmes automatiques pour le calcul d’implant.
Plusieurs publications montrent que la reproductibilité et la précision de ces appareils autorisent leur utilisation pour le calcul d’implant, à condition de vérifier la valeur de l’indice de conversion entre millimètres et dioptries [3, 33]. Tous les réfractomètres mesurent le rayon de courbure cornéen antérieur puis le convertissent en puissance pour traduire l’association des deux dioptres cornéens antérieur et postérieur. Cette conversion se fait par le biais d’un indice qui représente, encore à l’heure actuelle, une source de discussion. L’indice de réfraction utilisé par les appareils de type Javal est de 1,3333, alors que les appareils reposant sur le principe Bausch & Lomb utilisent un indice de 1,3375. D’autres indices sont utilisés pour différents appareils, rendant un peu plus complexe la standardisation des mesures. Il est donc nécessaire de vérifier cette valeur sur l’instrument de kératométrie ou bien d’utiliser les données de la kératométrie en millimètres dans le calculateur d’implant pour limiter le risque de fluctuation, par exemple dans des sites de consultation disposant de différents appareils de kératométrie.
La kératométrie par IOLMaster® est prise sur six points de mesure sur un diamètre de 2,5 mm avec un système automatique d’aide à la fiabilité des mesures. Ces mesures sont prises sur trois axes fixes permettant ensuite, par calcul, de déterminer la puissance et l’axe des deux méridiens principaux.
La comparaison avec les résultats obtenus par kératométrie se fait souvent sur des moyennes, avec de bonnes corrélations entre les deux systèmes de mesure. Cependant, les variations individuelles des mesures peuvent être importantes, témoignant ainsi de la différence de principe de mesures prises, de surcroît, sur des diamètres sensiblement différents (2,5 mm contre 3 mm).
Cette différence générée par le système IOLMaster® est intelligemment compensée par l’adaptation de la constante A, incluant les différences de mesure de kératométrie et de longueur axiale par rapport au mode de calcul fondé sur la kératométrie classique et le mode ultrasonore. Cet élément est d’autant plus optimisé que l’important déploiement de ces appareils a permis une certaine standardisation des mesures ainsi qu’une analyse comparable des mesures prises sur de nombreux sites de consultation.
L’appareil Lenstar® apporte une majoration du nombre de points de mesure, avec des mires projetées sur deux cercles concentriques de 1,7 et 2,1 mm de diamètre bénéficiant chacun de seize points de mesures soit trente-deux points de mesure en tout. Les méridiens principaux et leurs puissances sont alors recalculés. Les approximations entre deux points de mesure sont moins importantes qu’avec l’IOLMaster® mais la mesure est prise de façon plus centrale que l’IOLMaster® et nettement plus centrale que les kératomètres. Une adaptation de la constante A sera probablement nécessaire pour tenir compte de cet élément.
Le développement des systèmes de topographie cornéenne, avec la possibilité de prendre des mesures de rayons de courbure en de très nombreux points de la cornée, donne une meilleure appréciation du pouvoir optique de l’aire centrocornéenne (fig. 14-1) [24]. Cependant, la valeur à retenir pour le calcul d’implant n’est pas encore clairement définie. La valeur le plus couramment utilisée est la moyenne du rayon de courbure sur les 3 mm centraux [26]. Mais la moyenne des points en regard de l’aire pupillaire ou l’équivalent de la kératométrie peuvent aussi être utilisés. À la difficulté du choix de la valeur à retenir pour le calcul d’implant se rajoute le problème de la diversité des appareillages. Les publications qui comparent les différents résultats le font en utilisant un kératomètre de référence dont les valeurs sont rapportées aux mesures de topographie cornéenne réalisées avec un appareil donné. Les conclusions des articles qui traitent de ce sujet ne valent donc que pour un couple d’appareillage donné. Pour transposer en pratique courante l’utilisation d’un système de topographie cornéenne, il est donc souhaitable de comparer les différentes valeurs kératométriques du vidéokératoscope à celles couramment obtenues avec l’appareil classique habituellement utilisé.
Les progrès des appareils récents de topographie cornéenne portent sur des cartographies d’élévation entre une sphère idéale et la courbure de la cornée soit sur sa face antérieure soit sur sa face postérieure. Cette possibilité est offerte par différents appareils dont les plus connus sont le topographe Orbscan® (Baush & Lomb) (fig. 14-1) et le Pentacam® (Oculus).
Les mesures dérivées du rayon de courbure postérieur peuvent venir en support de l’appréciation de la puissance cornéenne, notamment en cas de calcul d’implant après chirurgie réfractive.
La kératométrie reste un élément important du calcul d’implant, avec une nécessité de précision accrue du fait de l’amélioration de la précision de toute la chaîne de mesure, laissant un peu plus apparaître les imprécisions relatives de chaque mesure. La diversité des principes de mesure rajoute une variable sur le résultat réfractif postopératoire. De façon à limiter cette variabilité, il semble prudent, sur un site donné, d’utiliser un appareil de référence et d’adapter la constante A en fonction de l’appareil utilisé.
À l’heure actuelle, la force de la kératométrie automatisée est sa diffusion à large échelle et sa relative reproductibilité. La kératométrie par le système IOLMaster® de Zeiss bénéficie aussi d’une importante base de données comparative, permettant de recaler la constante A de façon spécifique. Les appareils plus récents comme le Lenstar® (Haag-Streit) suivront le même chemin, de façon à qualifier toute la chaîne de mesure.
En marge du calcul de la puissance de l’implant, les appareils de topographie cornéenne permettent une très bonne qualification de la puissance et de l’axe de l’astigmatisme cornéen. Cet élément est crucial lors du recours aux implants toriques.

Fig. 14-1 Orbscan®.
L’apport de la topographie cornéenne est de donner une topographie des rayons de courbure en précisant la régularité ou l’irrégularité de ces rayons de courbure. Cet élément est rendu possible grâce aux nombreux points de mesure, contrairement au kératomètre qui ne mesure la puissance cornéenne que sur les deux méridiens principaux.
La mesure de référence pour la longueur axiale a longtemps été obtenue par échographie en mode A. Cette technique échographique, très largement utilisée, peut bénéficier d’un gain en précision par recours au mode B. Les progrès récents en matière d’interférométrie et la large diffusion de l’appareil IOLMaster®, et plus récemment du Lenstar®, permettent d’améliorer la précision des mesures de longueur axiale et leur reproductibilité, devenant progressivement la référence par rapport aux systèmes de mesure par ultrasons [10, 16, 32].
Pendant de nombreuses années, les biomètres les plus utilisés ont été les appareils d’échographie en mode A qui traduisent en pics de différentes hauteurs les structures plus ou moins échogènes traversées par le faisceau ultrasonore (fig. 14-2).
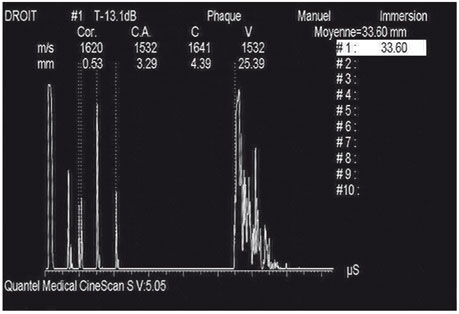
Fig. 14-2 Échographie mode A.
Exemple de biométrie en mode A qui identifie les pics des différentes interfaces avec des montées très abruptes témoignant d’une bonne perpendicularité du faisceau ultrasonore par rapport aux interfaces du cristallin et de la rétine. Cet élément est un gage de fiabilité de mesure.
La longueur axiale mesurée par échographie doit correspondre à la distance entre l’interface cornéenne antérieure et l’interface rétinovitréenne sur l’axe visuel.
Les formules théoriques de calcul d’implant utilisent une valeur légèrement différente, la longueur axiale optique, qui est la distance entre le plan principal optique secondaire de la cornée et le plan des photorécepteurs rétiniens. La position du plan principal optique secondaire de la cornée fait l’objet d’un relatif consensus à 50 µm en arrière de la face cornéenne antérieure. Au contraire, la position du plan des photorécepteurs fait l’objet de quelques controverses autour de l’épaisseur de la rétine maculaire : la valeur de 250 µm, choisie par Binkhorst, est la plus communément utilisée depuis 1981. Les formules de calcul rajoutent automatiquement cette valeur à la longueur axiale obtenue car la mesure de longueur axiale par échographie est prise au niveau de l’interface vitréorétinienne.
La biométrie en mode A peut se pratiquer en mode de contact cornéen ou bien en mode d’immersion pour identifier l’interface cornéenne antérieure et éviter de déformer la cornée – ce qui peut conduire à une réduction artificielle de la longueur axiale ; cette compression cornéenne entraîne une erreur relative plus importante pour les globes courts.
La sonde est positionnée sur le centre de la cornée de façon à viser la macula. Le faisceau ultrasonore traverse la cornée, la chambre antérieure, le cristallin et le vitré avant d’arriver à l’interface rétinovitréenne. Chaque interface traversée se traduit par un pic dont la hauteur varie avec la réflectivité de l’interface.
Classiquement, un échogramme de biométrie le plus fiable possible doit montrer des pics principaux, cristalliniens et rétiniens, les plus hauts possibles. La conversion de l’échogramme A en mesures de distance se fait par positionnement de repères qui identifient différents secteurs intraoculaires dans lesquels les ultrasons se propagent à une vitesse connue. Les appareils les plus utilisés ont quatre repères pour identifier trois segments intraoculaires (tableau 14-I) :
– le segment compris entre la face antérieure de la cornée et la face antérieure du cristallin est converti en distance selon une vitesse de conduction des ultrasons de 1 532 m · s–1 ;
– le segment cristallinien est converti selon une vitesse de conduction de 1 641 m · s–1 ;
– le segment vitréen est converti selon une vitesse de 1 532 m · s–1.
La vitesse de conduction dans le cristallin fait l’objet de discussions, surtout liées au fait que cette vitesse varie avec le vieillissement. Coleman a mesuré une vitesse de 1 659 m · s–1 à l’âge d’un an et de 1 629 m · s–1 à soixante-douze ans [4].
Sur certains appareils, un repère supplémentaire permet d’individualiser le segment cornéen avec une vitesse de conduction de 1 640 m · s–1.
À l’opposé, certains appareils ne possèdent que deux repères à positionner l’un sur le pic cornéen antérieur, l’autre sur le pic rétinien avec une vitesse de conduction moyenne de 1 555 m · s–1. En raison de cette simplification, plusieurs approximations sont proposées pour tenir compte la longueur axiale et de l’épaississement progressif du cristallin avec l’âge.
Classiquement, lorsque la mesure est prise en mode contact, il est conseillé de réaliser plusieurs mesures et de retenir la valeur de longueur axiale la plus élevée. Cependant, il est souhaitable de tenir compte de la valeur moyenne notamment pour les globes myopes pour lesquels la valeur la plus longue ne correspond pas toujours à la mesure sur l’axe visuel.
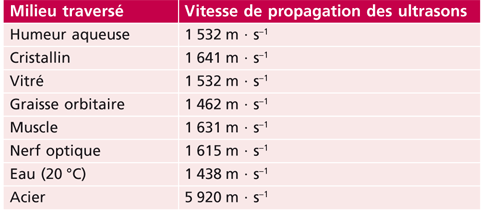
Tableau 14-I Vélocités de Coleman.
Ce tableau montre les différences de vitesse de conduction des ultrasons dans les différents tissus intraoculaires. La connaissance de ces vitesses de conduction permet de convertir le temps de propagation des ultrasons, mesuré par les échographes dans les différents tissus, en distance
La biométrie en mode A est une technique de mise en œuvre assez simple qui est réalisée en position assise lors de l’examen à la lampe à fente. Les appareils modernes enregistrent rapidement une série de mesures grâce au mode automatique. Cependant, il est nécessaire de contrôler cet automatisme, notamment pour le positionnement des surbrillances, qui peut parfois être imprécis. En effet, que ce soit en mode manuel ou automatique, il est parfois difficile d’individualiser les différentes interfaces pour positionner les repères de mesures. Cela est le cas lorsqu’une cataracte dense se traduit par plusieurs échos intracristalliniens.
Le principal écueil du mode A réside dans la difficulté à réaliser la mesure sur l’axe visuel qu’aucun repère ne permet d’identifier, en dehors des montées franches des différents pics. Cette difficulté devient très pénalisante lorsqu’il s’agit de globes myopes avec un aspect de pôle postérieur déformé.
Il s’agit, en fait, d’une biométrie en mode A guidée par l’exploration oculaire en mode B [1]. L’immersion simplifiée, paupières ouvertes, évite la compression de la cornée. L’objectif est d’obtenir une coupe axiale horizontale qui va guider la mesure pour se rapprocher le plus possible de l’axe visuel. La coupe axiale horizontale passe par le sommet de la cornée, la pupille, la face antérieure du cristallin, la face postérieure du cristallin et le pôle postérieur repéré par la papille. Sur cette coupe, il est possible de superposer un vecteur de contrôle qui matérialise l’axe de mesure (fig. 14-3). L’axe visuel faisant un angle de 15° avec la papille, il faut décaler le vecteur de contrôle de 15° en temporal de la papille. Le vecteur de contrôle peut être instantanément transformé en échogramme A pour ensuite positionner les repères de vitesse de conduction des ultrasons, comme en mode A.
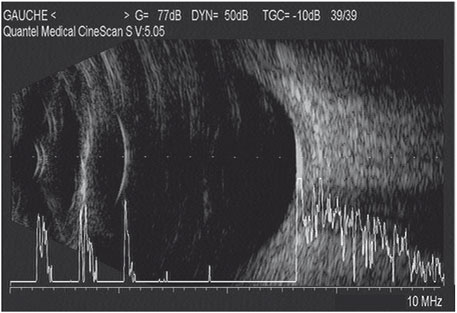
Fig. 14-3 Échographie mode B.
Exemple de biométrie en mode B réalisée en pseudo-immersion par interposition d’un gel de contact entre la sonde et la cornéen du patient. Cette méthode permet d’éviter l’écueil de la biométrie de contact. L’avantage de la biométrie en mode B réside dans la possibilité de guider l’axe de mesure de la longueur axiale et de recueillir toutes les mesures sur l’axe visuel sans limitation en fonction des différentes pertes de transparence des milieux.
La biométrie en mode B est pratiquée alors que le patient est en position allongée de façon à faciliter l’immersion. Le médecin est positionné à la tête du patient pour explorer les deux yeux indifféremment. Le patient regarde un point de fixation situé au plafond. Une petite quantité de gel de contact est placée sur la cornée pour positionner la sonde d’échographie en suspension en regard de l’apex cornéen.
La biométrie en mode B est une technique d’échographie qui donne une meilleure appréciation de la position de l’axe de mesure par rapport au mode A, ce qui améliore la précision de la mesure de longueur axiale et par conséquent la précision du calcul d’implant [2]. Cet avantage est surtout évident pour les globes déformés par un staphylome irrégulier (fig. 14-4) [5, 9].
Les limites du mode B résident dans l’impossibilité de visualiser la véritable position de l’axe visuel et de la fovéola.
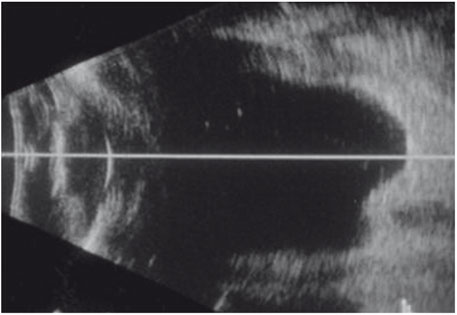
Fig. 14-4 Échographie mode B.
La biométrie en mode B permet de rendre fiables les mesures de longueur axiale, notamment en cas de staphylome myopique, avec l’avantage de réaliser un bilan des relations vitréorétiniennes. L’autre avantage est d’obtenir des mesures même en cas de perte de transparence des milieux.
En utilisant le principe de l’interférométrie déjà intégré dans la tomographie en cohérence optique (OCT), il est possible de prendre une mesure de longueur axiale par la voie d’un système optique. Cette technique, plus récente, est pratiquée en position assise avec une aide à la fixation du patient qui donne une meilleure coïncidence avec l’axe visuel. La précision de cette méthode de mesure dépend de la possibilité du système de traverser un cristallin cataracté, dont l’indice de réfraction optique peut varier en fonction du type de cataracte. La mesure de longueur axiale est réalisée entre la face antérieure de la cornée et l’interface entre photorécepteurs et épithélium pigmentaire. Ceci correspond à une longueur axiale plus longue que celle mesurée par échographie.
Une compensation est alors apportée systématiquement par les différents systèmes actuellement sur le marché.
Le premier appareil commercialisé a été l’appareil IOLMaster® (Zeiss-Meditec), avec une importante avance technologique au moment de son lancement : cet appareil compact est capable de prendre toutes les mesures nécessaires pour le calcul d’implant et de réaliser les différents calculs en incluant les principales formules (fig. 14-5). La kératométrie est mesurée sur six points, la longueur axiale est mesurée par interférométrie avec une reproductibilité et une précision très élevées, la profondeur de chambre antérieure est mesurée par reconnaissance de forme, la mesure de blanc à blanc est possible et les différents calculs sont possibles avec une interface conviviale.
Cet appareil ne mesurant pas exactement les mêmes valeurs que la biométrie classique, l’intelligence a été de proposer une personnalisation de la constante A et une formule entièrement adaptée à cette machine, en l’occurrence la formule de Haigis [13].
Un appareil plus récent, le Lenstar® (Haag-Streit), apporte un plus grand nombre de mesures par interférométrie (épaisseur cornéenne, profondeur de chambre antérieure, épaisseur du cristallin et longueur axiale) (fig. 14-6). Toutes ses mesures sont également mesurées par le mode ultrasonore, mais l’interférométrie, grâce à sa meilleure résolution, apporte un gain en précision très appréciable. La mesure de kératométrie se fait aussi différemment de l’appareil IOLMaster®. Ces éléments poussent à utiliser les constantes A avec prudence en début d’utilisation de cet appareil. La possibilité de mesurer l’épaisseur du cristallin ouvre la voie à l’utilisation des formules les plus récentes, comme la formule de Holladay 2 ou la formule d’Olsen, pour prévoir au mieux la position de l’implant après chirurgie de la cataracte.
Les appareils de mesure de longueur axiale fondés sur le principe de l’interférométrie souffrent cependant d’une limitation des possibilités de mesure en cas de perte de transparence des milieux (cataracte, hémorragie) ou de nystagmus. L’absence de réponse varie de 5 % à 12 % en fonction des séries publiées, avec une dépendance notable par rapport au recrutement de patients présentant des cataractes plus ou moins denses.
Il est probable que les avancées techniques actuelles sont annonciatrices d’autres évolutions de ces appareils et de l’arrivée d’autres fabricants pour le plus grand bénéfice de l’amélioration du calcul d’implant.

Fig. 14-5 Diagramme de mesures avec l’appareil IOLMaster® (Zeiss-Meditec).
Qualification des mesures par l’indice SNR (rapport signal sur bruit) : plus ce rapport est élevé, plus la mesure peut être considérée comme fiable.
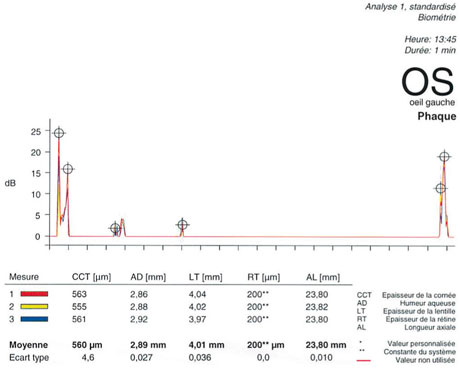
Fig. 14-6 Acquisition de mesures avec l’appareil Lenstar® (Haag-Streit).
L’avantage du Lenstar® est de donner des mesures de toutes les distances habituellement obtenues par le mode ultrasonore : la pachymétrie, la profondeur de la chambre antérieure, l’épaisseur du cristallin, la longueur axiale et même l’épaisseur de la rétine.
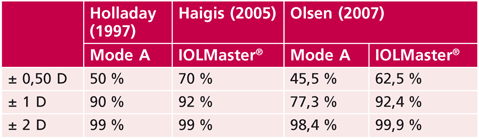
Tableau 14-II Précision réfractive de la biométrie.
Résultats publiés par Holladay et Olsen montrant la progression de la précision des mesures par l’arrivée de la biométrie optique. La tranche de résultats comprise entre ± 0,50 D est passée de 50 % à 70 % en dix ans, mettant en évidence une importante amélioration des résultats mais laissant cependant 30 % des patients avec un risque d’erreur réfractive résiduelle supérieure à 0,50 D. Cet élément est à prendre en compte en cas d’utilisation d’implants multifocaux.
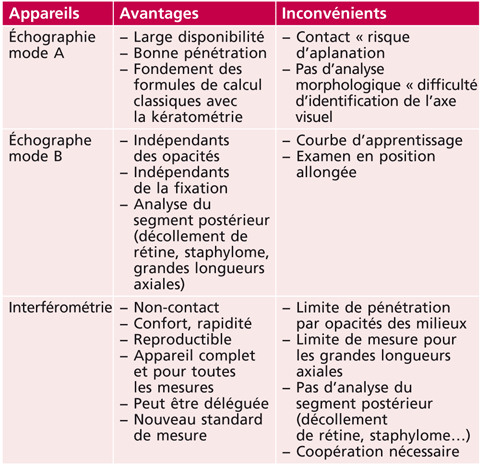
Tableau 14-III Avantages et inconvénients de chaque appareil.
La qualité, la géométrie et surtout la position de l’implant jouent un rôle essentiel dans le calcul d’implant. Dans un esprit de simplification des calculs, les formules utilisent des constantes qui représentent l’ensemble des paramètres de l’implant.
La forme de l’implant joue un rôle dans la position des plans optiques principaux de l’implant. Les implants plan-convexes ou biconvexes n’ont pas le même facteur de forme pour retrouver la position du plan principal de l’implant. De même, l’épaisseur de l’implant va jouer un rôle dans son positionnement. La relation entre la forme de l’optique de l’implant et la forme des haptiques ainsi que l’angulation des différentes parties de l’implant sont des éléments essentiels pour le positionnement de l’implant. Les implants multifocaux nécessitent une attention toute particulière quant à leur capacité à se positionner à une distance prévisible par rapport à la cornée.
Il peut jouer un rôle important dans la réfraction finale : d’une part la flexibilité de l’implant peut influencer la position de l’optique de l’implant dans le sac cristallinien, d’autre part à chaque matériau correspond un indice de réfraction qui retentit sur le pouvoir optique de l’implant [19].
Elle fait l’objet de nombreuses publications et représente l’élément essentiel dans la prédictibilité de la réfraction postopératoire [11, 27, 28]. La position de l’implant est le seul élément des formules de calcul qui ne peut pas être mesuré en préopératoire. Les formules de régression ont inclus ce paramètre dans la constante A. Une variation de 0,5 mm dans le positionnement axial de l’optique d’un implant de 20 D entraîne environ 1 D d’erreur réfractive postopératoire [25, 26]. Les améliorations des formules théoriques portent sur une meilleure appréciation de la position de l’implant. Cette position est de plus en plus corrélée à la longueur axiale, à la profondeur de chambre antérieure préopératoire, à l’épaisseur du cristallin et au diamètre cornéen. Par exemple la formule de Haigis tient compte du rayon de courbure de la cornée dans sa constante a0, de la profondeur de chambre antérieure mesurée en préopératoire dans la constante a1 et de la longueur axiale dans la constante a2.
Ces constantes représentent une variable d’ajustement qui permet d’adapter le calcul de l’implant à la fois à une procédure de calcul d’implant donnée mais aussi à la réponse obtenue en acuité visuelle après plusieurs séries statistiques de patients [23].
La constante A, comme les autres constantes, permet de caractériser un modèle d’implant et de réunir plusieurs paramètres en une seule valeur qui pourra être personnalisée par chaque chirurgien en fonction de sa chaîne de prise de mesures préopératoires, de sa technique chirurgicale et de ses résultats postopératoires.
La constante A, qui est la plus utilisée, a été décrite en 1980 avec les formules de régression et a longtemps reposé sur les mesures prises par échographie en mode A de contact [23]. Son appellation est souvent formulée en « constante A ultrasonore ». Elle est exprimée en dioptries pour satisfaire aux unités de grandeur de la formule SRK. Deux types d’implants avec une même constante A devraient donc être interchangeables avec le même résultat réfractif. Malheureusement, cette simplification n’est possible que pour des longueurs axiales proches de 21 mm et pour des implants dont l’épaisseur centrale, le facteur de forme et l’angulation entre haptique et optique sont comparables.
En 1988, Holladay a décrit le « surgeon factor » pour caractériser les différents modèles d’implants [20]. Cette constante correspond à la distance entre le plan irien pseudophaque et le plan principal de l’implant théorique. La notion de véritable position de l’implant a été introduite sous l’appellation anglaise de Effective Lens Position (ELP).
Hoffer a proposé d’appeler ce facteur ACD (Anterior Chamber Depth), qui correspond à la position de l’implant théorique par rapport au second plan principal de la cornée et non à la profondeur anatomique de la chambre antérieure en postopératoire [17].
Plus récemment, avec l’arrivée de l’appareil IOLMaster® et sa possibilité de mesure de la profondeur de chambre antérieure, Haigis a inclus dans sa formule un élément d’appréciation de la position de l’implant basé sur trois constantes dépendant chacune d’un paramètre différent : a0 est dépendant du rayon de courbure de la cornée, a1 est dépendant de la profondeur de chambre antérieure et a2 est dépendant de la longueur axiale [14]. Ces trois paramètres étant dépendants de la formule de Haigis et représentant trois valeurs supplémentaires à mémoriser, la notion de « constante A optique » a été développée. Cette constante A optique est celle qui est préconisée lorsqu’on utilise la formule SRK/T avec des mesures prises en IOLMaster®. L’utilisation de mesures provenant d’autres appareils comme le Lenstar® devront bénéficier d’une adaptation spécifique pour tenir compte de leurs mesures légèrement différentes.
L’avantage actuel du système IOLMaster® est de bénéficier de la mise en commun de nombreuses études de réfraction postopératoire avec des mesures reproductibles assez standardisées, quel que soit le lieu d’exercice. Le site internet ULIB met à la disposition des utilisateurs les mises à jour permanentes des constantes.
La myopie forte se traduit par une déformation axiale de la coque oculaire qui pose des problèmes de prise des mesures de longueur axiale. La déformation du pôle postérieur par le staphylome myopique peut entraîner des erreurs de biométrie, car les repères de mesure en échographie en mode A deviennent imprécis, surtout en cas de staphylome situé en nasal de la papille avec la macula se présentant de façon oblique par rapport au faisceau ultrasonore [5, 6, 9]. La biométrie en mode B permet, dans ce cas, d’améliorer la localisation de la macula mais il n’est pas possible, en l’état actuel de la technique, de localiser précisément la fovéola. La technique de cohérence optique, grâce à son point de fixation, permet une mesure sur l’axe visuel, limitant ainsi les aléas de mesure de longueur axiale. Les appareils optiques sont cependant limités dans la mesure des grandes longueurs axiales avec une limite technique à 40 mm pour le IOLMaster® et 32 mm pour le Lenstar®.
Le calcul d’implant en cas de forte hypermétropie pose différents problèmes. En ce qui concerne la biométrie, il est fortement recommandé d’utiliser une technique sans contact par interférométrie ou un mode ultrasonore en immersion pour éviter la compression de la cornée, qui se traduit par une erreur relative plus importante sur les globes courts.
L’anatomie des globes très courts peut soit correspondre à des yeux microphtalmes, avec un segment antérieur de taille réduite ainsi qu’un segment postérieur court, soit à des globes avec un segment antérieur de taille comparable aux yeux emmétropes mais avec un segment postérieur très raccourci. Pour rendre compte de cette différence, Holladay, Haigis et Olsen ont intégré dans leurs formules de calcul plus de mesures préopératoires, comme la profondeur de chambre antérieure préopératoire, le diamètre cornéen de blanc à blanc et l’épaisseur du cristallin (pour Olsen et Holladay 2) [15, 22, 28].
Le facteur des formules théoriques correspondant à l’épaisseur de la rétine doit être modifié pour tenir compte de l’épaisseur rétinienne plus importante.
Le déplacement antéropostérieur de l’implant entraîne une erreur réfractive plus importante : pour un implant de 40 D déplacé dans le sens antéropostérieur de 0,5 mm, l’erreur réfractive sera de 2 D.
La forte puissance des implants pour hypermétrope représente aussi une difficulté de fabrication des implants avec, pour certains, des aberrations optiques assez marquées. Les progrès de fabrication des implants actuels permettent cependant de répondre à la majorité des situations, ce qui évite le recours proposé il y a quelques années à l’implantation en piggyback qui consiste à positionner deux implants, avec un implant de forte puissance dans le sac cristallinien, puis un second implant dans le sulcus ciliaire [22]. Cependant, cette méthode peut être très utile pour l’adjonction d’un implant multifocal sur un globe déjà opéré de cataracte avec implant dans le sac cristallinien (cf. chapitre 19).


[1] Berges O., Puech M., Assouline M. et al. B-mode-guided vector-A-mode versus A-mode biometry to determine axial length and intraocular lens power. J Cataract Refract Surg, 1998 ; 24 : 529-35.
[2] Binkhorst R.D. The accuracy of ultrasonic measurement of the axial length of the eye. Ophthalmic Surg, 1981 ; 12 : 363-5.
[3] Butcher J.M., O’Brien C. The reproducibility of biometry and keratometry measurements. Eye (Lond), 1991 ; 5 : 708-11.
[4] Coleman D.J., Lizzi F.L., Franzen L.A., Abramson D.H. Determination of the velocity of ultrasound in cataractous lenses: ultrasonography in ophthalmology. Bibl Ophthalmol, 1975 ; 83 : 246.
[5] Curtin B.J. The natural history of posterior staphyloma development. Doc Ophthalmol Proc Ser, 1981 ; 28 : 207-13.
[6] Drexler W., Findl O., Schmetterer L. et al. Eye elongation during accommodation in humans: differences between emmetropes and myopes. Invest Ophthalmol Vis Sci, 1998 ; 39 : 2140-7.
[7] Fyodorov S.N., Kolinko A.I., Kolinko A.I. Estimation of optical power of the intraocular lens. Vestn Oftalmol, 1967 ; 80 : 27-31.
[8] Fenzl R.E., Gills J.P., Cherchio M. Refractive and visual outcome of hyperopic cataract cases operated on before and after implementation of the Holladay II formula. Ophthalmology, 1998 ; 105 : 1759-64.
[9] Fernandez-Vigo J., Castro J., Diaz J., Cip M.R. Ultrasonic forms of posterior staphyloma. Ann Ophthalmol, 1990 ; 22 : 391-4.
[10] Findl O., Drexler W., Menapace R. et al. High precision biometry of pseudophakic eyes using partial coherence interferometry. J Cataract Refract Surg, 1998 ; 24 : 1087-93.
[11] Findl O., Drexler W., Menapace R. et al. Accurate determination of effective lens position and lens-capsule distance with 4 intraocular lenses. J Cataract Refract Surg, 1998 ; 24 : 1094-8.
[12] Gauss C.F. Dioptrische Untersuchungen. Druck und Verlag der Dieterichschen Buchhandlung, Göttingen, 1841.
[13] Haigis W. Optical coherence biometry. Dev Ophthalmol, 2002 ; 34 : 119-30.
[14] Haigis W. Intraocular lens calculation after refractive surgery for myopia: Haigis-L formula. J Cataract Refract Surg, 2008 ; 34 : 1658-63.
[15] Haigis W. [IOL calculation for high ametropia]. Ophthalmologe, 2008 ; 105 : 999-1004.
[16] Haigis W., Lege B., Miller N., Schneider B. Comparison of immersion ultrasound biometry and partial coherence interferometry for intraocular lens calculation according to Haigis. Graefes Arch Clin Exp Ophthalmol, 2000 ; 238 : 765-73.
[17] Hoffer K.J. The Hoffer Q formula: a comparison of theoretic and regression formulas. J Cataract Refract Surg, 1993 ; 19 : 700-12.
[18] Holladay J.T., Prager T.C., Chandler T.Y., Musgrove K.H. A three-part system for refining intraocular lens power calculations. J Cataract Refract Surg, 1988 ; 14 : 17-24.
[19] Holladay J.T., Ting A.C., Koester C.J. et al. Silicone intraocular lens resolution in air and in water. J Cataract Refract Surg, 1988 ; 14 : 657-9.
[20] Holladay J.T., Cravy T.V., Koch D.D. Calculating the surgically induced refractive change following ocular surgery. J Cataract Refract Surg, 1992 ; 18 : 429-43.
[21] Holladay J.T., Hoffer K.J. Intraocular lens power calculations for multifocal intraocular lenses. Am J Ophthalmol, 1992 ; 114 : 405-8.
[22] Holladay J.T., Gills J.P., Leidlen J., Cherchio M. Achieving emmetropia in extremely short eyes with two piggyback posterior chamber intraocular lenses. Ophthalmology, 1996 ; 103 : 1118-23.
[23] Holladay J.T. Standardizing constants for ultrasonic biometry, keratometry, and intraocular lens power calculations. J Cataract Refract Surg, 1997 ; 23 : 1356-70.
[24] McQueen B.R., Martinez C.E., Klyce S.D. Corneal topography in cataract surgery. Curr Opin Ophthalmol, 1997 ; 8 : 22-8.
[25] Norrby S. Sources of error in intraocular lens power calculation. J Cataract Refract Surg, 2008 ; 34 : 368-76.
[26] Olsen T. Sources of error in intraocular lens power calculation. J Cataract Refract Surg, 1992 ; 18 : 125-9.
[27] Olsen T., Olesen H., Thim K., Corydon L. Prediction of pseudophakic anterior chamber depth with the newer IOL calculation formulas. J Cataract Refract Surg, 1992 ; 18 : 280-5.
[28] Olsen T., Corydon L., Gimbel H. Intraocular lens power calculation with an improved anterior chamber depth prediction algorithm. J Cataract Refract Surg, 1995 ; 21 : 313-9.
[29] Retzlaff J.A. A new intraocular lens calculation formula. J Am Intraocul Implant Soc, 1980 ; 6 : 148-52.
[30] Retzlaff J.A., Sanders D.R., Kraff M.C. Development of the SRK/T intraocular lens implant power calculation formula. J Cataract Refract Surg, 1990 ; 16 : 333-40.
[31] Sanders D.R., Retzlaff J., Kraff M.C. Comparison of the SRK II formula and other second generation formulas. J Cataract Refract Surg, 1988 ; 14 : 136-41.
[32] Shammas H.J. A comparison of immersion and contact techniques for axial length measurement. J Am Intraocul Implant Soc, 1984 ; 10 : 444-7.
[33] Shammas H.J., Chan S. Precision of biometry, keratometry, and refractive measurements with a partial coherence interferometry-keratometry device. J Cataract Refract Surg, 2010 ; 36 : 1474-8.

