Rotation fields and the fundamental theorem of Riemannian geometry in - 15/02/08

Doi : 10.1016/j.crma.2006.08.007

Philippe G. Ciarlet ^a , Liliana Gratie ^b , Oana Iosifescu ^c , Cristinel Mardare ^d , Claude Vallée e
^a Department of Mathematics, City University of Hong Kong, 83, Tat Chee Avenue, Kowloon, Hong Kong
^b Liu Bie Ju Centre for Mathematical Sciences, City University of Hong Kong, 83, Tat Chee Avenue, Kowloon, Hong Kong
^c Départment de mathématiques, université de Montpellier II, place Eugène-Bataillon, 34095 Montpellier cedex 5, France
^d Laboratoire Jacques-Louis Lions, université Pierre et Marie Curie, 4, place Jussieu, 75005 Paris, France
^e Laboratoire de mécanique des solides, université de Poitiers, 86962 Futuroscope-Chasseneuil cedex, France

Bienvenue sur EM-consulte, la référence des professionnels de santé.
L’accès au texte intégral de cet article nécessite un abonnement.

pages	7
Iconographies	0
Vidéos	0
Autres	0

Abstract

Let 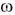be a simply-connected open subset of . We show in this Note that, if a smooth enough field U of symmetric and positive-definite matrices of order three satisfies the compatibility relation (due to C. Vallée)
CURL+COF=0in , where the matrix field 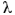is defined in terms of the field U by=1detU{U(CURLU)TU-12(tr[U(CURLU)T])U}, then there exists, typically in spaces such as or , an immersion such that in 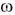. In this approach, one directly seeks the polar factorization of the gradient of the unknown immersion in terms of a rotation R and a pure stretch U. To cite this article: P.G. Ciarlet et al., C. R. Acad. Sci. Paris, Ser. I 343 (2006).

Le texte complet de cet article est disponible en PDF.

Résumé

. Soit 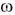un ouvert simplement connexe de . On montre dans cette Note que, si un champ suffisamment régulier U de matrices symétriques définies positives dʼordre trois satisfait la relation de compatibilité (due à C. Vallée)
CURL+COF=0dans, où le champ 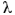de matrices est défini en fonction du champ U par=1detU{U(CURLU)TU-12(tr[U(CURLU)T])U}, alors il existe, typiquement dans des espaces tels que ou , une immersion telle que in 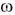. Dans cette approche, on cherche à identifier directement la factorisation polaire du gradient de lʼimmersion inconnue en une rotation R et une extension pure . Pour citer cet article : P.G. Ciarlet et al., C. R. Acad. Sci. Paris, Ser. I 343 (2006).